A deeper revisit to building heap - Building heap in O(n).

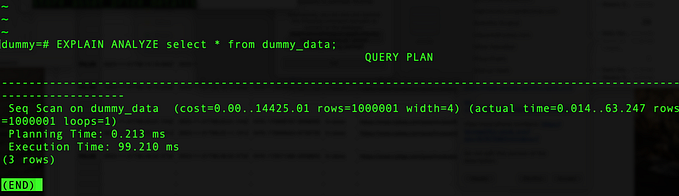
Heap sort: The sorting algorithm that requires no extra space and runs in O(nlogn). Heap sort acquires this time complexity from O(n) of BUILD_MAX_HEAP and O(nlog(n)) from (n-1) calls to MAX_HEAPIFY (log(n) for each call) consequently leading to the overall complexity of O(nlog(n)).

Let’s do a quick recap of heap sort.

Heapsort (A, n)
1. BUILD-MAX-HEAP(A, n)
2. for i = n downto 2
3.   exchange A[1] with A[i]
4.   A:heap-size  = A:heap-size - 1
5.   MAX-HEAPIFY (A, 1)

BUILD-MAX-HEAP (A, n)
1. A:heap-size = n
2. for i = ⌊n/2⌋ downto 1
3.   MAX-HEAPIFY (A, i)

MAX-HEAPIFY (A, i)
1. l = LEFT(i)
2. r = RIGHT(i)
3. if l <= A:heap-size and A[l] > A[i]
4.     largest = l
5. else largest = i
6. if r <= A:heap-size and A[r] > A[largest]
7.    largest = r
8. if largest != i
9.    exchange A[i] with A[largest]
10.   MAX-HEAPIFY (A, largest)

LEFT (i)
1. return 2*i

RIGHT (i)
1. return 2*i + 1

Having gone through it, do you puzzle over why (n-1) calls to MAX-HEAPIFY takes O(nlogn) in heap sort while it takes O(n) when called n/2 times in BUILD-MAX-HEAP?
Well, this is because the O(n) is tighter asymptotic bound of BUILD-MAX-HEAP. However, concluding BUILD-MAX-HEAP as O(nlogn) is not wrong. But following calculations give us more precise bound.

Note:

1. Don’t skip the proof (please!). It just requires basic understanding of summation and estimation. We are summing over all the nodes in the heap.
2. In the following calculation, ⌈n/2ʰ⁺¹⌉ is the no. of nodes in heap at height h. And so if takes O(h) time for a node at h, then for all the nodes at height h it will take ⌈n/2ʰ⁺¹⌉*h time. (c is a constant in the proof) Hence, c*⌈n/2ʰ⁺¹⌉*h for all nodes at height h. Now, let’s sum it over for h(height) = 0 to logn i.e.
   Σˡᵒᵍⁿₕ₌₀c*⌈n/2ʰ⁺¹⌉*h

Source: Introduction.to.Algorithms 4th Leiserson Stein Rivest Cormen

If ⌈n/2ʰ⁺¹ ⌉≥ 1/2 for 0 ≤ h ≤ ⌈logn⌉ bothered you, I got you covered! Here’s, the proof.

The solution is not mine. It has been taken from https://quizlet.com/latest.

Hope you found something to learn. This logic can be extended to the problems which require building a heap structure from an unorderd array.
Anyway, a brownie point is always coming if you bring this tighter bound during the discussion! :-P
Do let me know what all could and could not be there.